Задания к занятию 1
Ответы
6, 12, 18, 24.

Арлекин съел один пирожок, Буратино — 3, Пьеро — 11, Артемон — 13 пирожков.
$4\frac{1}{13}$.
а) Да; б) нет.
Белоснежка, в 3 раза.
7.
300.
6 и 9.
10.
Условия задач
Найдите все натуральные числа, при делении которых на 5 в частном получается то же самое число, что и в остатке.
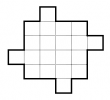
Разрежьте фигуру, изображённую на рисунке, на 4 одинаковые части. Найдите как можно больше решений.
Мальвина испекла 30 пирожков и угощает ими Пьеро, Буратино, Артемона и Арлекина. Через некоторое время оказалось, что Буратино и Пьеро съели столько же, сколько Артемон и Арлекин, а Пьеро и Артемон — в 6 раз больше, чем Буратино и Арлекин. Какое количество пирожков съел каждый, если Арлекин съел меньше всех остальных? (Все съедали пирожки целиком, и каждый съел хотя бы один пирожок.)
Найдите значение выражения $4\frac{2}{7}:1\frac{5}{21}+\left(4\frac{3}{13}\cdot\frac{14}{15}-3\frac{1}{3}\right).$
Маша разрезала лист бумаги на 3 части. После этого она взяла один из кусков и тоже разрезала на 3 части. Потом опять один из кусков разрезала на 3 части и т.д. Могло ли оказаться так, что лист бумаги в итоге разрезан: а) на 2019 частей; б) на 2020 частей?
Белоснежка с двумя гномами сажала цветы в саду. После того, как в ним присоединились ещё 5 гномов, скорость посадки цветов увеличилась в 2 раза. Кто быстрее сажает цветы и во сколько раз: Белоснежка или гном? Все гномы сажают цветы с одинаковой скоростью.
7 волков съедают 7 баранов за 7 дней. За сколько дней 9 волков съедят 9 баранов?
Мама купила коробку кускового сахара (сахар в кубиках). Дети сначала съели верхний слой — 77 кубиков, затем боковой слой — 55 кубиков, наконец, передний слой. Сколько кубиков сахара осталось в коробке?
Второклассники Андрей, Боря, Витя, Гриша и Денис по очереди верно решили пять примеров из таблицы умножения. Каждый следующий мальчик получил ответ в полтора раза больше предыдущего. Какие числа умножал Гриша?
Сколько существует девятизначных чисел, цифры которых расположены в порядке убывания?